Research
Exploration of the basic flow phenomena
The focus is on investigating basic flow phenomena of incident and confined shear driven and natural convection flows including the linear stability analysis, numerical simulation of slightly bifurcated flows, developing novel techniques for tackling and characterizing turbulent flows.
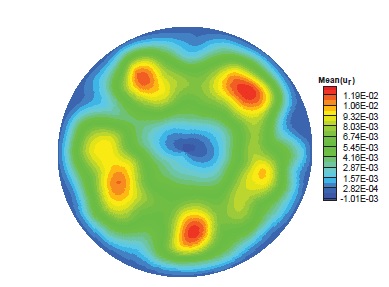
Turbulence in a localized puff in a pipe. The analysis is based on the results acquired by the direct numerical simulations of transient turbulence in pipe. The trailing edge of the puff hosts coherent structures which can be determined by calculating ensemble average of the radial velocity
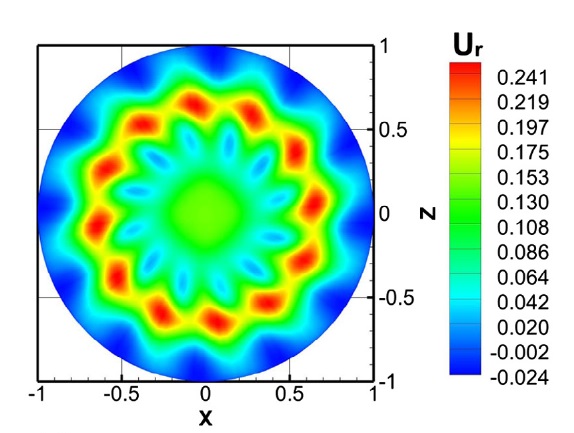
Laminar and turbulent convection in spherical shells (see link). The study is focused on investigation of laminar and turbulent convection inside concentric spherical shells up to Rayleigh number values and Pr=0.71. We have developed a new correlation for the heat transfer rate for both lamionar and trurbulent flow regimes.
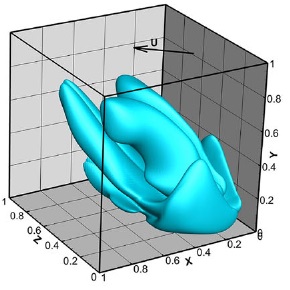
Theoretical analysis of three-dimensional bifurcated flow inside a diagonally lid-driven cavity (see link). The study investigates the instability mechanism of fully three-dimensional, highly separated, shear-driven confined flow inside a diagonally lid-driven cavity. An oscillatory regime of the bifurcated flow is observed and thoroughly characterized, revealing and characterizing the spontaneous symmetry breaking mechanism.
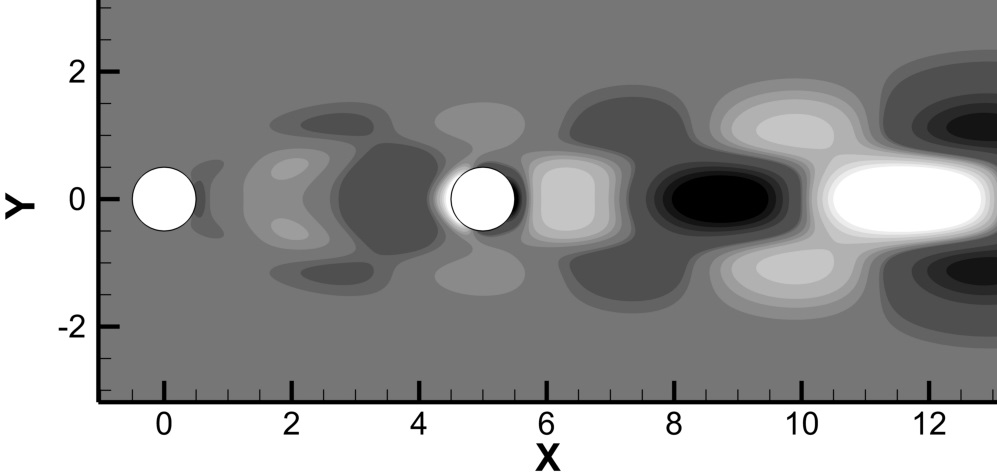 Investigating periodic incident flow around tandem of immersed bodies (see link). The study investigates and characterizes the various oscillating regimes of incident and confined natural convection flows around tandem of immersed bodies
Investigating periodic incident flow around tandem of immersed bodies (see link). The study investigates and characterizes the various oscillating regimes of incident and confined natural convection flows around tandem of immersed bodies
Development of novel numerical methods
The purpose is to develop robust accurate and highly scalable numerical techniques allowing for simulation of complex flow phenomena. We primarily focus on DNS (Direct Numerical Simulation) resolving all the flow scales without turbulence modeling.
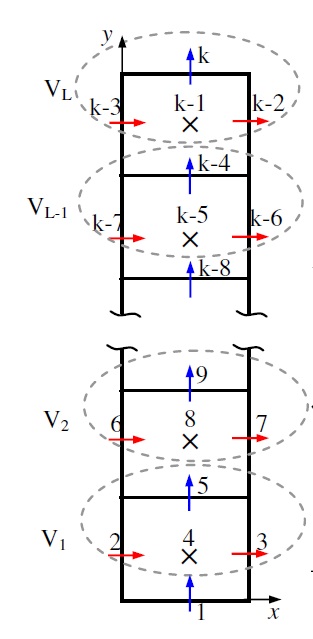
Accelerated Semi Implicit – Coupled Line Gauss Seidel ASA-CLGS Smoother (see link). The smoother is developed as a part of geometric multigrid algorithm and provides an exact solution for all the velocity and pressure corrections of the entire column (or row) of the final volumes
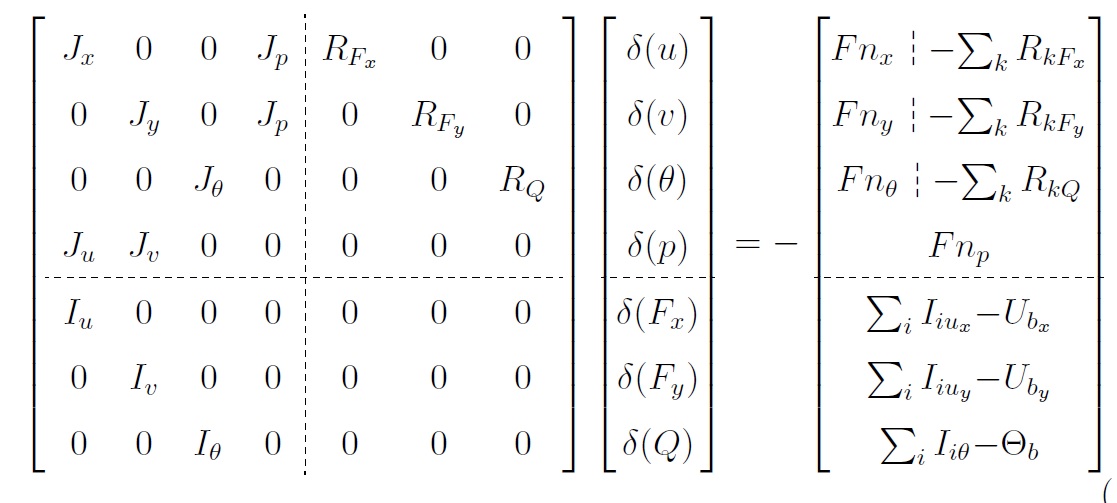 Extended immersed boundary method based on the Distributed Lagrange multiplier approach (see link)
Extended immersed boundary method based on the Distributed Lagrange multiplier approach (see link)
The method treats pressure, the Lagrangian forces, and heat sources as distributed Lagrange multipliers, thereby implicitly providing the kinematic constraints of no-slip and the corresponding thermal boundary conditions for immersed surfaces. It allows for DNS of natural convection and incident flows in the presence of a large number of immersed bodies. The developed approach also allows for accurate calculation of the steady state and its further linear stability analysis.
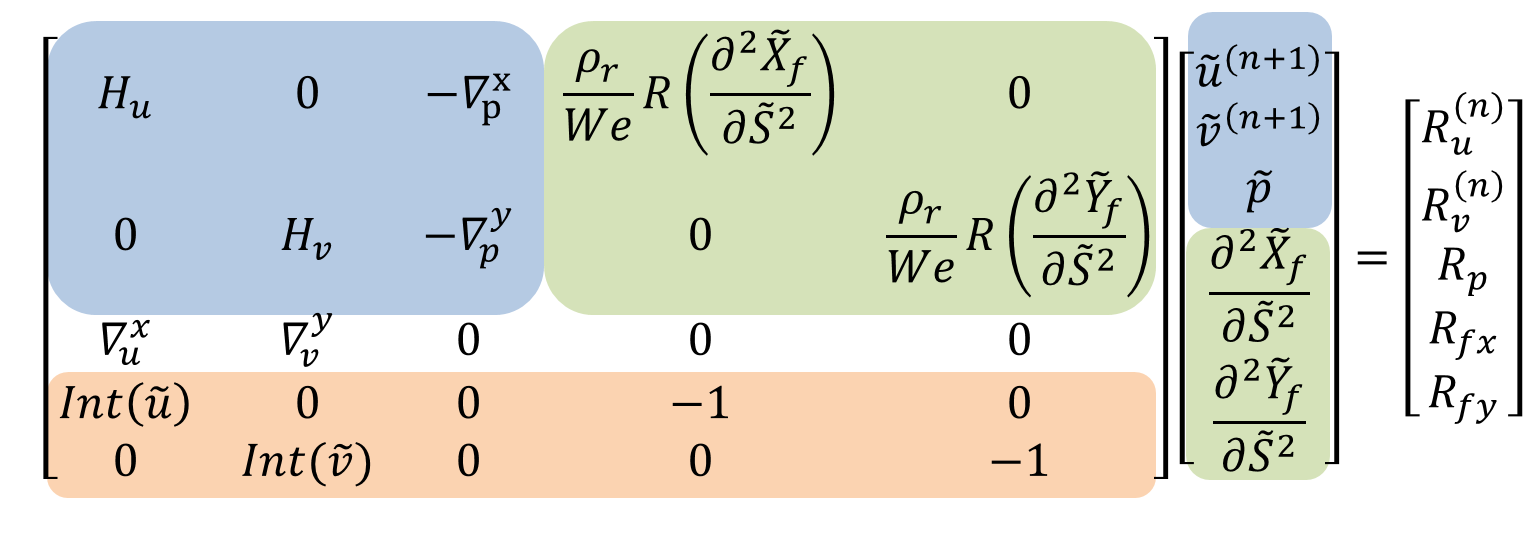 Immersed boundary method based on the Distributed Lagrange multiplier approach extended to simulation of immiscible 2-phase flows. The solver utilizes surface tension forces as Lagrange multipliers enforcing non-immiscibility of both phases as a kinematic constraint.
Immersed boundary method based on the Distributed Lagrange multiplier approach extended to simulation of immiscible 2-phase flows. The solver utilizes surface tension forces as Lagrange multipliers enforcing non-immiscibility of both phases as a kinematic constraint.
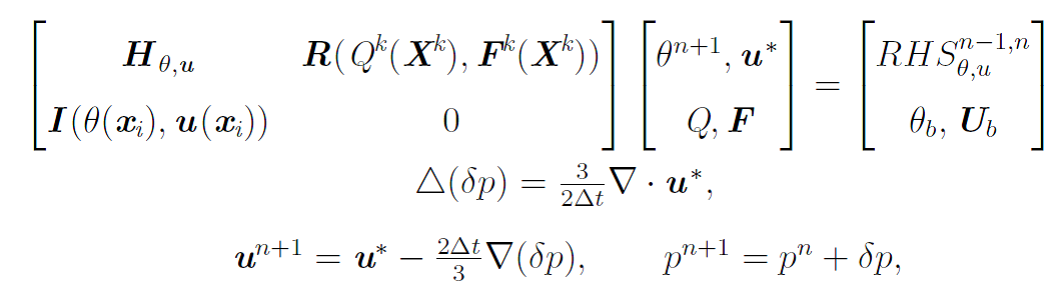 Implicit direct forcing immersed boundary method for incompressible viscous thermal flow problems: a Schur complement approach.
Implicit direct forcing immersed boundary method for incompressible viscous thermal flow problems: a Schur complement approach.
The developed tool can be straight forwardly plugged in into any existing time marching solver of incompressible Navier-Stokes equations based on a segregated pressure- velocity coupling.
Engineering applications
The tools developed by our group are successfully applied to analysis and design of various engineering applications.
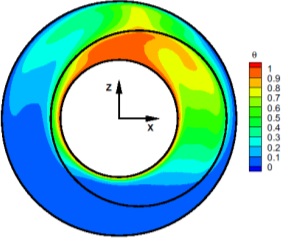 Efficient insulation of differentially heated spherical gap (see link). We proposed multilayered insulation of the differentially heated spherical shell. The study was performed for the spherical shell containing up
Efficient insulation of differentially heated spherical gap (see link). We proposed multilayered insulation of the differentially heated spherical shell. The study was performed for the spherical shell containing up
up to five walls and included both concentric and eccentric configurations.
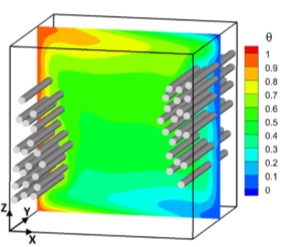 Deriving a concept of smart thermal insulation of 3d differntially heated rectangular containers. We established a concept of "smart" thermal insulating material based on heterogeneous porous media. The idea is based on a formal linear stability analysis revealing the most energetic regions of the flow. The momentuf of the flow in these regians is then subsequently suppressed by embeding heterogeneous porous media.
Deriving a concept of smart thermal insulation of 3d differntially heated rectangular containers. We established a concept of "smart" thermal insulating material based on heterogeneous porous media. The idea is based on a formal linear stability analysis revealing the most energetic regions of the flow. The momentuf of the flow in these regians is then subsequently suppressed by embeding heterogeneous porous media.